Fractals Tilings And Substitutions - A Fascinating Mathematical World!

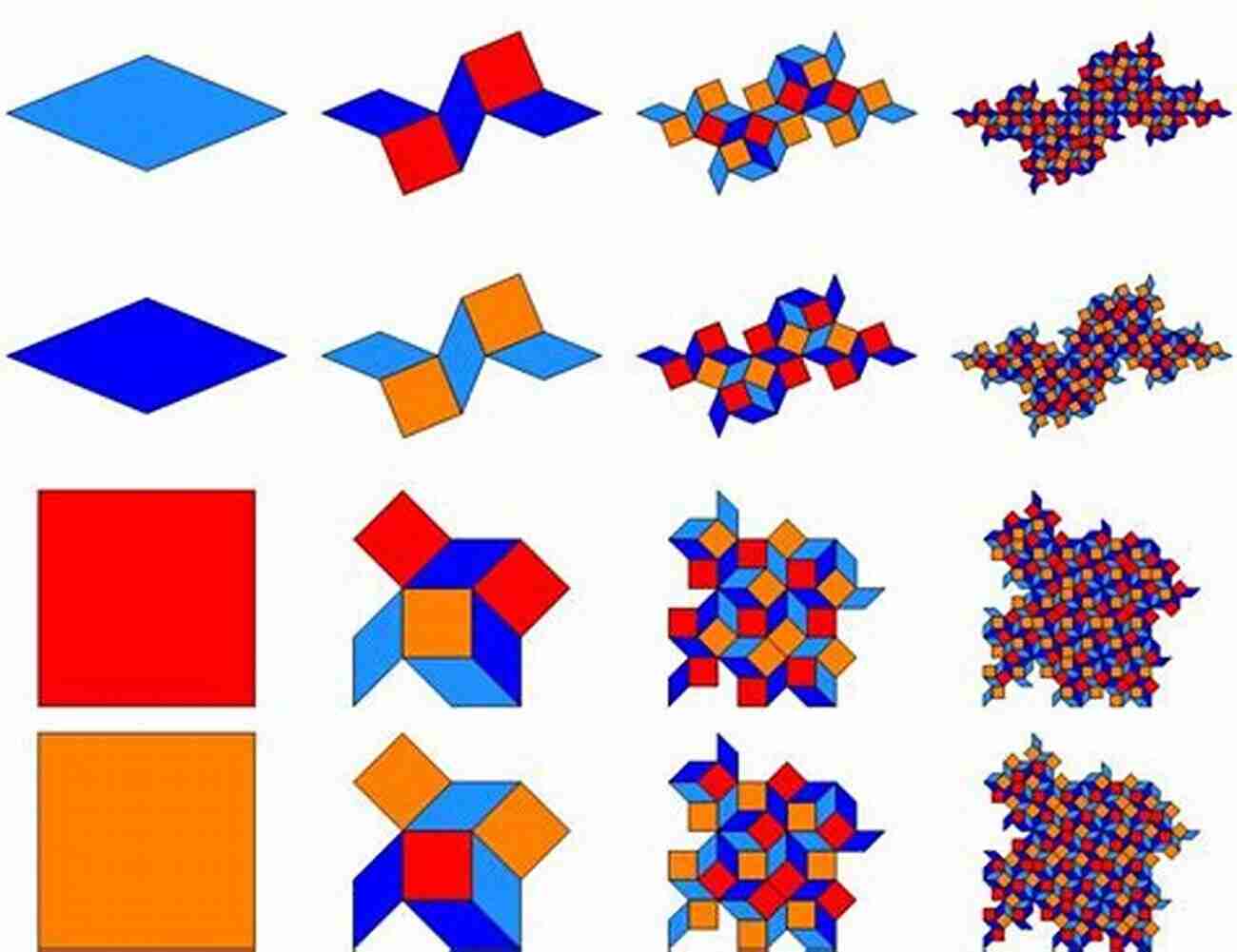
Fractals, tilings, and substitutions are captivating subjects within the field of mathematics. In this article, we will explore the intricate world of fractals, their properties, and their applications in various fields. We will also delve into tilings, their patterns, and the mesmerizing ideas behind them. Finally, we will discuss the concept of substitutions and their significance in mathematical analysis. If you have a passion for mathematics or are simply curious about these topics, read on!

Understanding Fractals

Fractals are complex, infinitely self-similar patterns found abundantly in nature and can be generated mathematically. They are objects that exhibit the property of self-similarity at different levels of magnification. The most famous example of a fractal is the Mandelbrot set, discovered by Benoit Mandelbrot in 1980. This visually stunning set displays incredible intricate patterns within patterns.

The study of fractals and their dimensions provides valuable insights into the irregular and complex shapes found in nature. Fractals have applications in computer graphics, data compression, and even in simulating natural phenomena such as clouds and mountains. They have also found important applications in physics, biology, and economics.

Chaotic Dynamics: Fractals, Tilings, and Substitutions (Cambridge Mathematical Textbooks)

by MEI(1st Edition, Kindle Edition)

5 out of 5

Language	:	English
File size	:	31523 KB
Text-to-Speech	:	Enabled
Enhanced typesetting	:	Enabled
Print length	:	419 pages
Screen Reader	:	Supported

FREE

Tiling the World

Tilings refer to covering a flat surface with distinct shapes without any gaps or overlaps. The fascinating world of tilings involves exploring a wide range of patterns, including regular and irregular tessellations. Artists, architects, and designers have drawn inspiration from these patterns for centuries.

Regular tessellations consist of congruent shapes that can cover a surface without any gaps or overlaps, forming repeating patterns. The most well-known example of a regular tiling is the Penrose tiling, discovered by Sir Roger Penrose in the 1970s. This tiling exhibits non-periodic patterns, which means they do not repeat themselves.

Irregular tessellations, on the other hand, involve the use of different shapes and can create visually stunning and intricate designs. These tilings have been used in various forms of art, from Islamic mosaics to modern abstract paintings. Understanding the underlying mathematics behind these patterns can lead to exciting discoveries and innovations.

Substitutions and Mathematical Analysis

Substitutions are mathematical operations that involve replacing one object with another according to specified rules. They play a crucial role in mathematical analysis and can help understand the behavior of complex systems.

One well-known substitution system is the Fibonacci sequence, where each number is the sum of the two preceding numbers. This sequence has numerous intriguing properties and can be found in various natural phenomena, including the growth patterns of trees and the arrangement of seeds in a sunflower.

Another fascinating example is the Sierpinski triangle, which is constructed through a substitution process. Starting with an equilateral triangle, smaller triangles are recursively removed, resulting in a self-similar pattern at multiple levels of magnification.

Substitutions provide valuable insights into the underlying structure and behavior of complex systems, making them essential tools for mathematicians, physicists, and scientists in various fields. They also have applications in cryptography, coding theory, and the study of dynamical systems.

Discover the Beauty of Mathematics!

Fractals, tilings, and substitutions open up a fascinating mathematical world filled with breathtaking patterns and mind-boggling concepts. Exploring these subjects can ignite a sense of wonder and curiosity about the universe we live in.

If you are interested in diving deeper into these topics, "Fractals Tilings And Substitutions" by Peter R. A. Mansfield, one of the renowned Cambridge Mathematical Textbooks, is an excellent resource. This comprehensive textbook provides a rigorous yet accessible to these subjects, taking readers on an exciting journey through their history, properties, and applications.

Whether you are a student, a mathematician, or simply someone who appreciates the beauty of mathematics, consider delving into the captivating world of fractals, tilings, and substitutions. The more we understand these concepts, the better we can unravel the mysteries of our universe and appreciate the elegance of mathematics.

Chaotic Dynamics: Fractals, Tilings, and Substitutions (Cambridge Mathematical Textbooks)

by MEI(1st Edition, Kindle Edition)

5 out of 5

Language	:	English
File size	:	31523 KB
Text-to-Speech	:	Enabled
Enhanced typesetting	:	Enabled
Print length	:	419 pages
Screen Reader	:	Supported

FREE

This undergraduate textbook is a rigorous mathematical to dynamical systems and an accessible guide for students transitioning from calculus to advanced mathematics. It has many student-friendly features, such as graded exercises that range from straightforward to more difficult with hints, and includes concrete applications of real analysis and metric space theory to dynamical problems. Proofs are complete and carefully explained, and there is opportunity to practice manipulating algebraic expressions in an applied context of dynamical problems. After presenting a foundation in one-dimensional dynamical systems, the text introduces students to advanced subjects in the latter chapters, such as topological and symbolic dynamics. It includes two-dimensional dynamics, Sharkovsky's theorem, and the theory of substitutions, and takes special care in covering Newton's method. Mathematica code is available online, so that students can see implementation of many of the dynamical aspects of the text.