Unlocking the Secrets of Mathematical Proof: Examples, Solutions, and Insights

Mathematical proofs are the backbone of the world of mathematics. They provide a way to rigorously demonstrate the truth or validity of a mathematical statement. These proofs allow mathematicians to build upon established knowledge and explore new frontiers in various branches of mathematics.

The Importance of Mathematical Proof

Mathematical proof is a fundamental aspect of mathematics, serving several crucial purposes:

• Verification: A proof provides certainty and confidence in the truth of a mathematical statement. It ensures that a claim can be universally accepted as valid.
• Understanding: Proofs allow mathematicians to gain a deeper insight into the underlying principles and concepts of a mathematical statement.
• Problem Solving: Proofs are an essential tool for solving mathematical problems. They provide logical steps to arrive at a solution and can inspire new problem-solving techniques.

Elements of a Mathematical Proof

A mathematical proof consists of several elements that work together to establish the validity of a statement. These elements include:

Understanding Proof: Explanation, Examples and Solutions of Mathematical Proof

by KEDAR PANDA(International ed. Edition, Kindle Edition)

4 out of 5

Language	:	English
File size	:	16849 KB
Text-to-Speech	:	Enabled
Screen Reader	:	Supported
Enhanced typesetting	:	Enabled
Print length	:	248 pages
Lending	:	Enabled

FREE

1. Assumptions: Every proof starts with a set of assumptions or previously proven statements that are accepted as true.
2. Definitions: Precise definitions of terms involved in the statement are crucial. These definitions provide the language and framework for the proof.
3. Lemmas: Intermediate results or supporting theorems that are used to derive the main result.
4. Axiomatic Statements: Statements that are accepted without proof, serving as the building blocks for further deductions.
5. Logical Reasoning: Arguments using deductive logic to draw s based on the assumptions, definitions, and axiomatic statements.
6. : The final step in the proof that wraps up the logical reasoning and establishes the truth of the original statement.

Example Proof: Pythagorean Theorem

Let's explore a classic example of a mathematical proof: the Pythagorean Theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

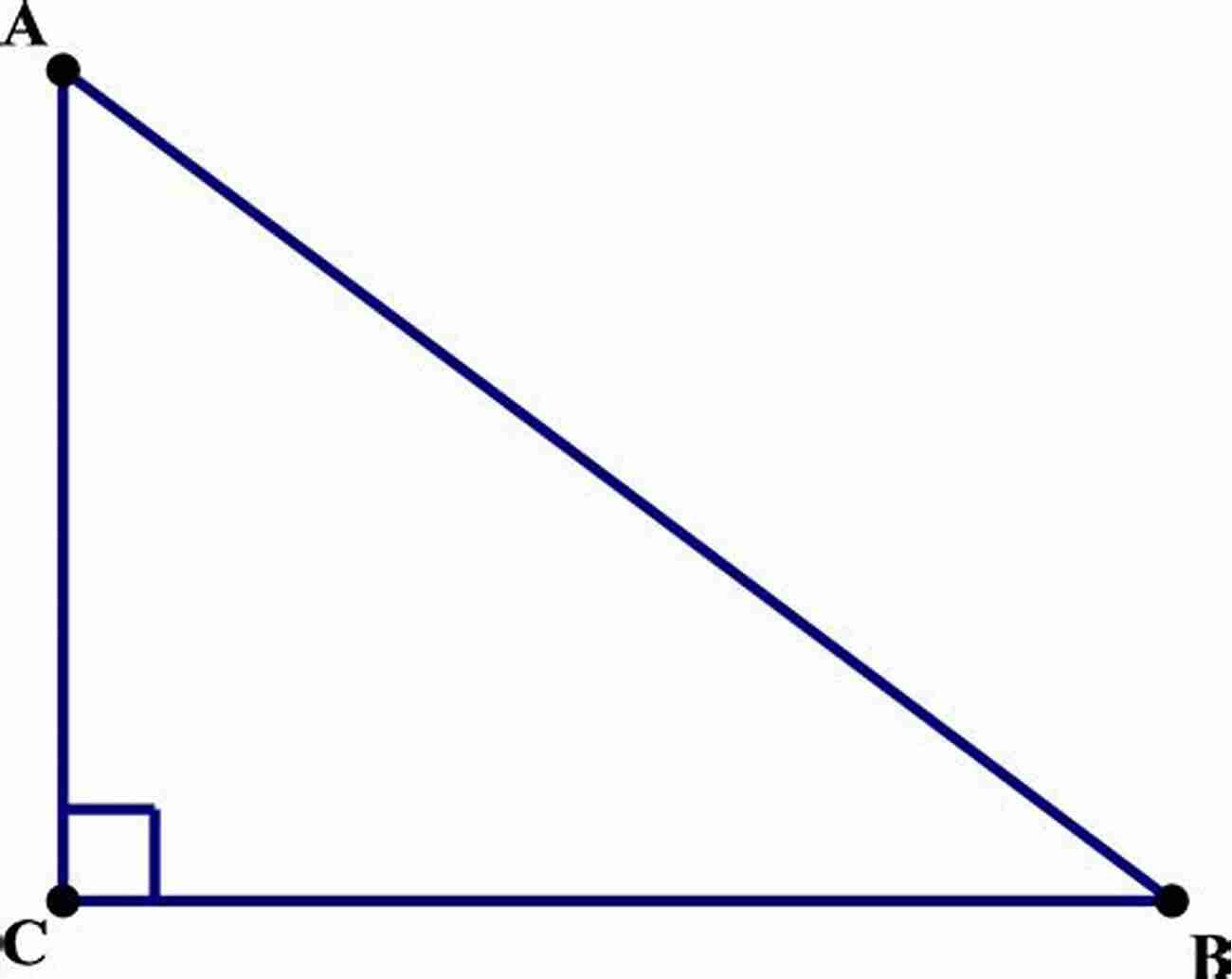
We start with a right-angled triangle ABC, where AB represents the hypotenuse and AC and BC are the other two sides. The lengths of AC and BC are denoted as a and b, respectively.

The proof involves constructing squares on each side of the triangle and using their areas to establish the relationship:

Step 1: Construct squares on AC and BC:

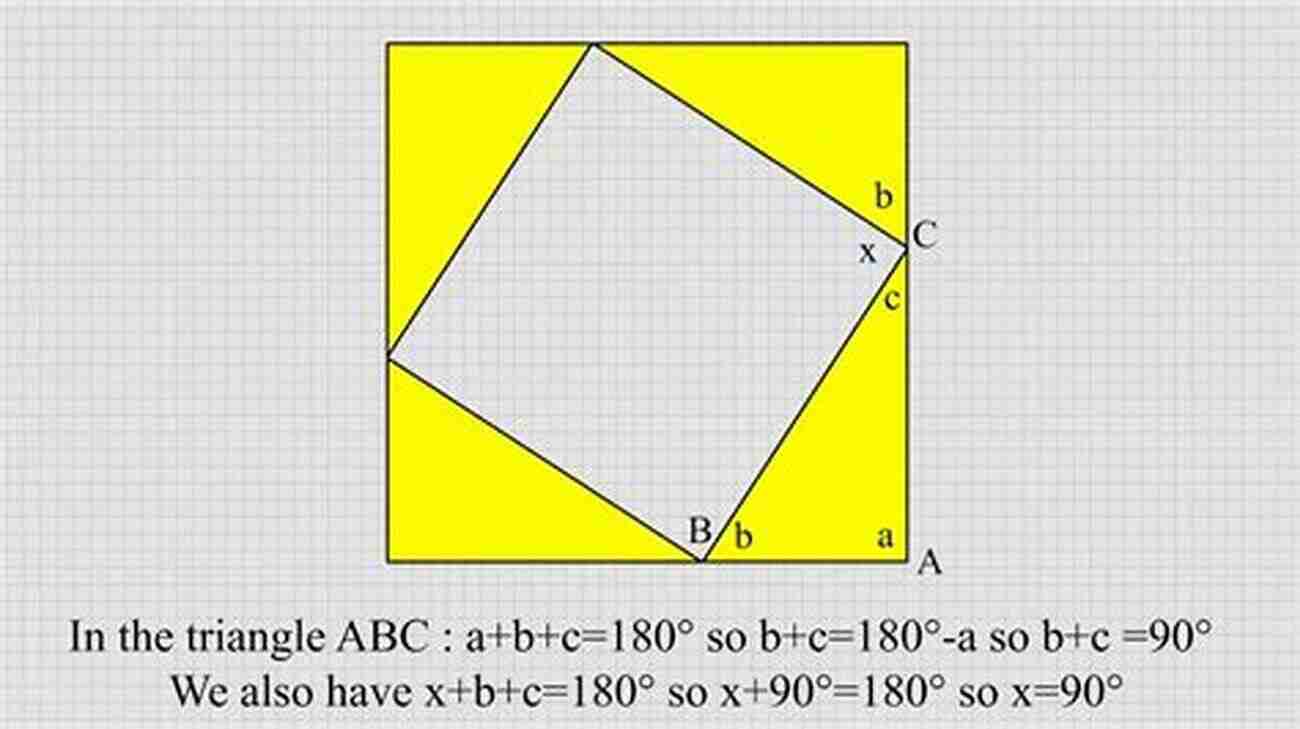
Step 2: Divide the squares into smaller squares and rearrange them:

Step 3: Compare the areas of the smaller squares:

The areas of the smaller squares can be represented as:

a² + b² + 4(½ab) = c² + 2(ab)

Step 4: Simplify the equation:

a² + b² + 2ab = c²

As the area of the square on AB is equal to the sum of the areas of the smaller squares, we have successfully shown that:

a² + b² = c²

Solutions to Common Proof Challenges

While mathematical proofs can be elegant and intellectually stimulating, they can also present challenges. Here are some common proof challenges and strategies to overcome them:

1. Lack of Direction: Sometimes, you may find yourself unsure of how to approach a proof. In such cases, it is helpful to start with specific examples and explore patterns that can guide you towards a general solution.
2. Complexity: Complex proofs often require breaking down the problem into smaller, more manageable parts. By tackling each component individually, you can gradually build towards a complete proof.
3. Assumptions: Occasionally, incorrect assumptions can lead to flawed proofs. Carefully examine the assumptions you are making and verify their validity before proceeding further. It is also essential to clearly state any assumptions made in your proof.
4. Counterexamples: Counterexamples can disprove a statement, highlighting the need for precise conditions or additional constraints in a proof. When faced with a potential counterexample, thoroughly analyze its properties and adjust your approach accordingly.

Mathematical proofs are not only vital for verifying the truth of mathematical statements but also for advancing our understanding and solving mathematical problems. With careful reasoning and the application of fundamental concepts, mathematicians unveil the hidden intricacies of the mathematical world. By studying and mastering the art of mathematical proof, one can embark on a journey of discovery and contribute to the ever-evolving field of mathematics.

Understanding Proof: Explanation, Examples and Solutions of Mathematical Proof

by KEDAR PANDA(International ed. Edition, Kindle Edition)

4 out of 5

Language	:	English
File size	:	16849 KB
Text-to-Speech	:	Enabled
Screen Reader	:	Supported
Enhanced typesetting	:	Enabled
Print length	:	248 pages
Lending	:	Enabled

FREE

Proof is central to any mathematics curriculum and indeed, all mathematical thinking. Now we are delighted to provide an International Edition of our guide to proof for students...and for their teachers too. Contents: to proof 2. Exploring Methods of Proof 3. Mathematical Language 4. Direct Proof 5. Indirect Proof 6. Proof by Induction 7. Proof and Applications of Pythagoras' Theorem 8. Proof in Calculus 9. Proving Trigonometric Identities 10. Proof in Statistics and Probability 11. Worked Solutions